Introduction

On todays modern websites, we often have sets of user-uploaded images. These are rarely all the same aspect ratio, so creating grids can be problematic. The two usual solutions are either to have a jagged grid or crops the images. If we preserve the aspect-ratio images and just resize them to a uniform height, the end result will be jagged edges because the rows will have different widths. To combat this, many people uses cropping, to ensure that all images have identical aspect-ratios (e.g. 4/3 or 16/9) and then scaling them to a identical size. This will produce a nice even grid, but because we have cropped the images to get the desired aspect-ratio we have lost information from the original photos.

So is there another way? Yes there is: Packing. By deciding which images should end up in which rows we can produce a desirable packing that will allow us to produce a nicely aligned grid. Depending on what criteria you have, calculating an optimal packing can vary from computationally simple to very complicated.

Background

Image packing can use multiple different ways of achieving a nice grid. Common for all approaches is that the first step is to find a optimal distribution of images to rows – ie, which images goes in which row. Depending on your criteria you might be able to freely choose which row an image should be placed in. If there is no restricting on the order the images must be reproduced in, it is a free-for-all. However, it is also very computationally intensive to find the ordering that gives the best packing.
Most uses for packing images in a grid require a determined ordering, which means that the distribution is a simple question of figuring out where to introduce line-breaks.

Once you have a distribution, you very likely still have rows of different widths. It would need to be a very fortunate set of images if merely distributing images on rows results in rows of equal lengths. Therefore rows needs some post-processing to ensure that they are of (roughly) equal width. A common approach is scaling the images on a row to ensure the row is the desired width. Another solutions would be either just leave the slightly irregular rows as-is and accept a slight jaggedness. Lastly a possible solution could include skewing or cropping the images to ensure both equal height and width of each row.

There are many well-known examples of packing images to produce visually nice listings. Two examples are Google Image Search, and Flickr. If we compare these, it is clear that Flickr heavily scales each row because the rows have very different heights. Unlike Google Image Search solution, this ensure that all rows have identical widths. Google seems to have opted for allowing slightly different widths, although Google still seems to be scaling each row because the rows do differ slightly in height. So it seems as if they have a limit to just how much they allowed the images to be scaled. Flickr seems as if they keep the original ordering of photos, and allow the user to change the sorting criteria. With Google it’s hard to judge just how the ordering is performed, so who knows if they rearrange the photos to get a better distribution between rows.

Problem Analysis

To design a packing algorithm, certain choices must be made regarding what criteria you want the packing to enforce. In this article I have chosen the following criteria, which seems identical to the properties enforced by Flickr.

1. All rows must be exactly the same width
2. All images within a row must have the same height
3. The ordering of the images must not change
4. All rows must be full – including the last row

The reason for the first two criteria is what ensures that the packing is going to look visually nice. It will be even looking rows without any jagged lines.
The motivation behind the last two criteria is to easily allow usage of the packing in listings of images. If we allowed the ordering to change, we could not use the packing in a listing sorted by e.g. time. Because we are using the packing in a listing, it will look visually much nicer to have all rows filled. Another reason for requiring filled line is that it will facilitate infinity- scrolling much more easily. If we were to load in the next page of the listing when the user scrolls near the button, it will be much easier if we just add a new set of rows to be appended, rather than possibly having to fill up the last row first.

Designing an Algorithm for Distribution of Images

As mentioned in Section 2, the first step to any image packing is distributing images on rows. Because I wish to retain the ordering of the images, this boils down to deciding where the line-breaks should be.

Now, we might envision a solution using a greedy algorithm that simply tries filling up a row with images, and then moves to the next row. This solution is very likely to end up with the last row not containing enough images to take up the desired width, which means it’s no good.
The next possibility is a class of algorithms called dynamic programming. Can we define an optimal solution as a combination of smaller optimal solutions – ie does the problem has an optimal substructure? And does the problem also have overlapping subproblems, causing us to need the optimal solution to a subproblem multiple times?

If we take a step back and look at our problem, what needs to be determined after each image is this: Is it better to have a line-break now or to add the next image to this row too.
Can we use a dynamic programming algorithm for this? Yes, because this is a problem with a optimal substructure, we can express the optimal solution using the optimal solution to one of two subproblems. And do we have overlapping subproblems? Yes, because both the optimal solution to packing four and five images depends on the optimal solution to packing 3 images.

So we can design a dynamic programming algorithm to solve this problem. For this we need a way to determine the contents a row. I have chosen to represent possible rows as a combination of starting image (i) and how many images are in a row (spree or s).
We can also determine how “bad” a row is, by calculating the difference between the desired width (d) and how wide a row would be. We call this difference the penalty. The penalty of the row starting with image i, containing s images is denoted P_i,s.
We also have notion of the combined penalty or the total cost of a packing. We call this cost C_i,s, which describe the cost of a packing that starts at image i, where the first row contains at least s images.
Lastly we denote the total number of images in the packing as n and the width of image i as w_i.

With these definitions of what P_i,s and C_i,s describes, we can formulate how to calculate them.

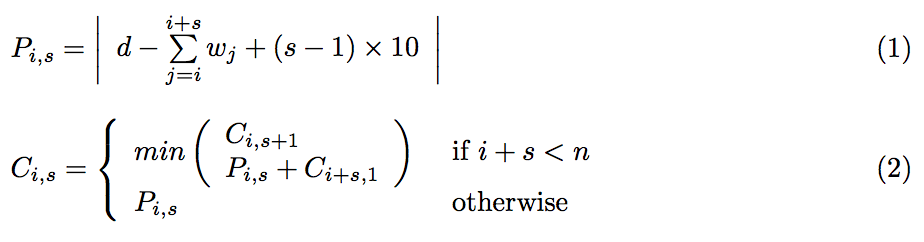
As we can see in Formula (1), the penalty is simply the absolute difference between the sum of the width of all images with a 10px gap between each. Somewhat more interesting is Formular (2) that states how the optimal (lowest) combined cost is calculated. It has two definitions: One when i + s = n (ie, there is no images left after this row) which is simply the penalty of this line. The second definition – when there is images not in the packing yet – is the minimum between the cost for including one more image in the current row (C_i,s+1) and the cost of having a line break. The cost of having a line-break is the combined cost of the current line (P_i,s) and the optimal cost of packing the remaining images (C_i+s,1).

With these two formulas we can define a function to calculate the optimal cost for packing the entire thing: C_0,1. This calculation can be performed either top-down or bottom-up. Top-down is equivalent to implementing the above mentioned formulas in a recursive fashion, possibly using memoization to speed up the solution of identical subproblems. A far more interesting approach is bottom-up, where we start out by calculating all the values without dependencies on any other values. Then we calculate the values that depends on those answers, and so forth. It is clear from the definition of C_i,s that it can be thought of as look-ups in a i × s table, where we only use the lower-left triangle (those where i + s ≤ n).

An example of such a table with n = 7 can be seen here:

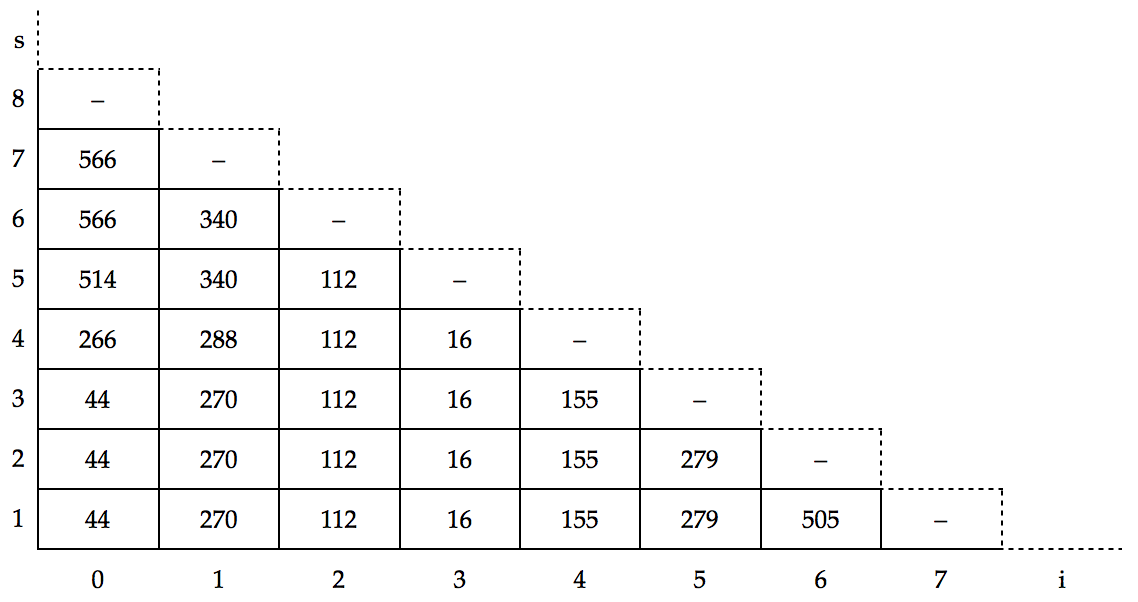
The calculations are simply performed top-to-bottom, right-to-left. So we start by calculating C_6,1 = P_6,1, then we move on to C_5,2 = P_5,2. When we know C_6,1 and C_5,2, we can calculate C_5,1 = min(C_5,2, P_5,2 + C_6,1 ) = C_5,2.
We can continue this way until we reach C_0,1, and then we are done.

Using the Algorithm to Determine a Distribution

The next question is how you go from this table over C_i,s, and produce a packing. This is simply done by starting at image i = 0, and moving up until the cost increases (in my example, it does after s = 3). When the cost increases, we introduce a line-break and start looking at image i = i + s. We continue this way untill i + s ≤ n
In my example the cost of image 3 never increases, so we only have the one line-break between image 3 and 4.

Using the packing data calculated, we end up with the following packing:

Post-Processing

As we can see above, it’s not that far off a optimal packing, but the two rows are slightly different widths. A simple post-processing of each row is used to even these differences out. This process is simply figuring out the scale (S_i,s) between how wide the row is and how wide is should be, and then scale each row accordingly:

The resulting, scaled, packing is:

Evaluation

I have proposed a solution that produced a image packing conforming to a certain set of criteria. In this section I will go through these properties one by one, to determine how well my proposed solution lives up to the requirements and what downsides introduced by ensuring this property.

All rows must be exactly the same width

The simple scaling post-process will always ensure that the images on a row are exactly the desired width. As you might imagine the amount of scaling that is performed is highly related to the desired width of the final packing. If the desired width is very low, only a few pictures can be fitted to each row, and thus the images must be scaled more to even out the gaps.

Having to scale the images by a large amount on the client-side can have implication on how the images look, especially if you are upscaling the images in the browser. It is possible to tweak the penalty function to favor overpacking each row, to force downscaling instead of upscaling.

All images within a row must have the same height

By scales all images on a row by the same amount my proposed solution ensures that if the images started out the same height, they will end up having the same height too.

The ordering of the images must not change

By only considering where to add line-breaks, my solution can never change the ordering of the images it packs.

All rows must be full – including the last row

The dynamic programing algorithm I proposed for determining the optimal packing ensures that the last row will always contain a full row. The drawback to this, is that smaller sets of images are likely to be scaled rather harshly.

If the combined width of images just under one and a half times the desired width, no line-breaks are introduced, and the pictures are scaled down considerably. Likewise, if the combined width is just over one and a half times the desired width, it is forced into two lines with considerable upscaling as a result.
The more images, and thus rows, and the wider the desired width, the less pronounced the required scaling will be.

Computational Complexity of the Algorithm

It is trivial to see from the description of the algorithm that the computational complexity of the algorithm is O(n²).
Likewise the space requirements for holding the cost table are O(n²).

Sample Implementation

To verify the correctness of the proposed solution, a sample implementation in JavaScript was developed. Without spending any time optimizing the solution – e.g. the penalty is calculated every time – the solution is decently fast. The sample dataset of 23 images is distributed to 6 rows in around 40-50ms.

The sample implementation can be found at:
http://sevengoslings.net/~fangel/packgrid/

Further Work

I would like to develop the sample implementation into a more mature library that can easily used in websites that desire to have a nice collage of images for their image listings.

Additionally I think it could be interesting to investigate other means of ensuring that the rows have uniform widths. For instance, a combination of skewing and/or cropping the images might be able produce rows with equal hight without much visible change to the photos.

Conclusion

I have proposed a dynamic programming algorithm for packing images in a grid of completely filled rows of uniform widths. By allowing each row to be of a different hight and finding the optimal placements of line-breaks the desired packing is achieved. By performing a scaling post-process each line is guaranteed to be exactly as wide as the desired width.

The proposed algorithm has shown to easily computed with minimal requirements for time and memory required to calculate the packing.

Acknowledgements

All images used here, and in the sample application are taken from Flickr Commons, which is a collection of old photos from contributing museums and institutions. There is no known copyright of the photos.